8.3 Trigonometric Ratios of Some Specific Angles

geometry, you are already familiar with the construction of angles of 30°, 45°, 60° and 90°.

we will find the values of the trigonometric ratios for these angles and, of course, for 0°.

Trigonometric Ratios of 45°

In ∆ ABC, right-angled at B, if one angle is 45°, then the other angle is also 45°, i.e., ∠ A = ∠ C = 45°

So,      BC = AB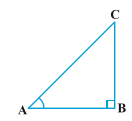Now, Suppose      BC = AB = a.

Then by Pythagoras Theorem, $$AC^{2} = AB^{2} + BC^{2} = a^{2} + a^{2} = 2a^{2}$$,

and, therefore,   $$AC=a\sqrt{2}$$

Using the definitions of the trigonometric ratios, we have :

$$Sin 45^{0}=\frac{side\:\: opposite\:\: to\:\: angle 45^{0}}{hypotenuse}=\frac{BC}{AC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$$

$$Cos 45^{0}=\frac{side\:\: adjacent\:\: to\:\: angle 45^{0}}{hypotenuse}=\frac{AB}{AC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$$

$$tan 45^{0}=\frac{side\:\: opposite\:\: to\:\: angle 45^{0}}{side\:\: adjacent\:\: to\:\: angle 45^{0}}=\frac{BC}{AB}=\frac{a}{a}=1$$

Also, $$cosec 45^{0}=\frac{1}{sin 45^{0}}=\sqrt{2}, sec45^{0}=\frac{1}{cos 45^{0}}=\sqrt{2}, cot 45^{0}=\frac{1}{tan 45^{0}}=1$$

Trigonometric Ratios of 30° and 60°

Let us now calculate the trigonometric ratios of 30° and 60°. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore, ∠ A = ∠ B = ∠ C = 60°.

Draw the perpendicular AD from A to the side BC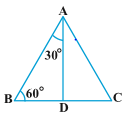Now               

∆ ABD ≅ ∆ ACD (Why?)

Therefore,             BD = DC

and                        ∠ BAD = ∠ CAD (CPCT)

Now observe that:

∆ ABD is a right triangle, right-angled at D with ∠ BAD = 30° and ∠ ABD = 60°

As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that AB = 2a.

Then, $$BD=\frac{1}{2}BC=a$$

And   $$AD^{2}=AB^{2}-BD^{2}=(2a)^{2}-(a)^{2}=3a^{2}$$.

Therefore,    $$AD=a\sqrt{3}$$

Now, we have:

$$Sin 30^{0}=\frac{BD}{AB}=\frac{a}{2a}=\frac{1}{2},\:\: cos 30^{0}=\frac{AD}{AB}=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}$$

$$tan 30^{0}=\frac{BD}{AD}=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}$$.

Also, $$cosec 30^{0}=\frac{1}{sin 30^{0}}=2, \:\:sec30^{0}=\frac{1}{cos 30^{0}}=\frac{2}{\sqrt{3}}$$

Cot $$30^{0}=\frac{1}{sin 30^{0}}=\sqrt{3}$$.

Similarly,

$$Sin 60^{0}=\frac{AD}{AB}=\frac{a\sqrt{3}}{2a},\:\: cos 60^{0}=\frac{1}{2}, tan 60^{0}=\sqrt{3}$$,

$$Cosec 60^{0}=\frac{2}{\sqrt{3}},\:\: sec 60^{0}=2 \:\:and \:\:cot 60^{0}=\frac{1}{\sqrt{3}}$$

Trigonometric Ratios of 0° and 90°

the trigonometric ratios of angle A, if it is made smaller and smaller in the right triangle ABC (see Fig. 8.16), till it becomes zero.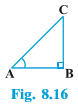As ∠A gets smaller and smaller, the length of the side BC decreases

The point C gets closer to point B, and finally when ∠ A becomes very close to 0°, AC becomes almost the same as AB (see Fig. 8.17).

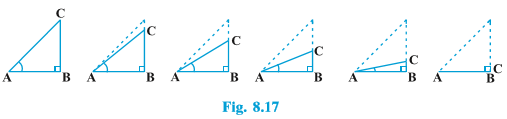When ∠ A is very close to 0°, BC gets very close to 0 and so the value of $$sin A =\frac{BC}{AC}$$

 is very close to 0. Also, when ∠ A is very close to 0°, AC is nearly the same as AB and so the value of $$cos A =\frac{AB}{AC}$$ is very close to 1.

This helps us to see how we can define the values of sin A and cos A when A = 0°. We define : sin 0° = 0 and cos 0° = 1.

Using these, we have :

$$tan 0^{0}=\frac{sin 0^{0}}{cos 0^{0}}=0, \:\:cot 0^{0}=\frac{1}{tan 0^{0}}$$, which is not defined.

$$Sec 0^{0}=\frac{1}{cos 0^{0}}=1  and\:\: cosec 0^{0}=\frac{1}{sin 0^{0}}$$, which is again not defines.

Now, let us see what happens to the trigonometric ratios of ∠ A, when it is made larger and larger in ∆ ABC till it becomes 90°.

As ∠ A gets larger and larger, ∠ C gets smaller and smaller.

Therefore, as in the case above, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠ A is very close to 90°, ∠ C becomes very close to 0° and the side AC almost coincides with side BC

When ∠ C is very close to 0°, ∠ A is very close to 90°, side AC is nearly the same as side BC, and so sin A is very close to 1. Also when ∠ A is very close to 90°, ∠ C is very close to 0°, and the side AB is nearly zero, so cos A is very close to 0.

So, we define : sin 90° = 1 and cos 90° = 0.

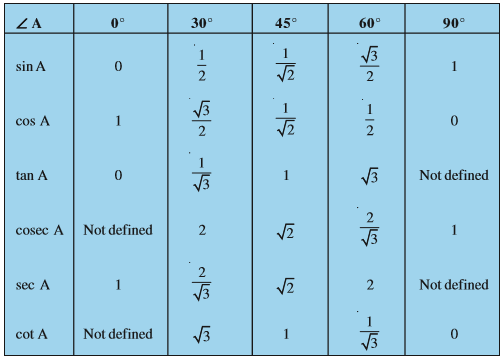
Example 6 : In ∆ ABC, right-angled at B, AB = 5 cm and ∠ ACB = 30° (see Fig. 8.19). Determine the lengths of the sides BC and AC.

Solution : To find the length of the side BC, we will choose the trigonometric ratio involving BC and the given side AB. Since BC is the side adjacent to angle C and AB is the side opposite to angle C, therefore

$$\frac{AB}{BC}=tan C$$i.e.,   $$\frac{5}{BC}=tan 30^{0}=\frac{1}{\sqrt{3}}$$

which gives        $$BC=5\sqrt{3}$$

To find the length of the side AC, we consider

$$Sin 30^{0}=\frac{AB}{AC}$$

i.e.,    $$\frac{1}{2}=\frac{5}{AC}$$

i.e.,     AC=10cm

Example 7 : In ∆ PQR, right-angled at Q (see Fig. 8.20), PQ = 3 cm and PR = 6 cm. Determine ∠ QPR and ∠ PRQ.

Solution : Given PQ = 3 cm and PR = 6 cm.

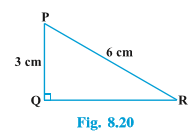Therefore,    $$\frac{PQ}{PR}=sin R$$

Or    $$sin R =\frac{3}{6}=\frac{1}{2}$$

So,    ∠ PRQ = 30°

and therefore, ∠ QPR = 60°.

Example 8 :If $$sin(A-B)=\frac{1}{2},\:\: cos(A+B)=\frac{1}{2}, \:\:0° < A + B ≤ 90°, \:\:A > B,\:\: find \:\:A \:\:and \:\:b$$.

Solution : Since, $$sin (A – B)=\frac{1}{2}$$, therefore, $$A-B=30^{0}$$………..(1)

Also, since $$cos (A + B) =\frac{1}{2}$$, therefore, A + B = 60°…………..(2)

Solving (1) and (2), we get : A = 45° and B = 15°.